

문제
동규부동산에서 아파트를 임대하고 있다. 아파트의 방은 아래 그림과 같이 면적이 2xy + x + y이다. (x와 y는 양의 정수)
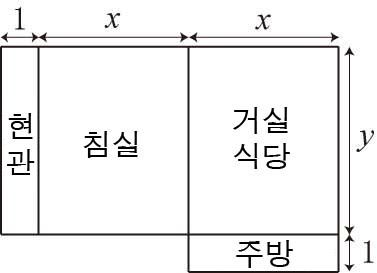
동규부동산의 카탈로그에는 아파트의 면적이 오름차순으로 적혀져 있지만, 이 중 일부는 있을 수 없는 크기의 아파트이다. 만약, 이런 크기의 아파트를 임대하겠다고 말하면, 동규는 꽝! 이라고 외치면서, 수수료만 떼어간다.
동규부동산의 카탈로그에 적힌 아파트의 면적이 주어졌을 때, 있을 수 없는 크기의 아파트의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 아파트의 면적의 수 N이 주어진다. 다음 줄부터 N개 줄에 카탈로그에 적혀있는 순서대로 면적이 주어진다. N은 100,000이하이고 면적은 231-1이하인 양의 정수이다.
출력
첫째 줄에 있을 수 없는 아파트 면적의 수를 출력한다.
예제
입력
10
4
7
9
10
12
13
16
17
19
20출력
2빠른 모듈러 거듭제곱법(Fast modular exponentiation)과 밀러-라빈 소수판별법(Miller-Rabin primality test)을 이용하여 문제를 풀었다.
두 알고리즘은 추후 포스팅하겠지만, 간략하게 소개하면
빠른 모듈러 거듭제곱법은 [a ^ b % m]의 형태의 수식을 빠른 시간안에 계산할 수 있는 방법이다.
밀러-라빈 소수판별법은 소수의 성질을 이용해 매우 큰 수도 빠른 시간안에 확률적으로 소수인지 판별할 수 있는 방법이다.
https://en.wikipedia.org/wiki/Miller%E2%80%93Rabin_primality_test
Miller–Rabin primality test - Wikipedia
From Wikipedia, the free encyclopedia Primality test The Miller–Rabin primality test or Rabin–Miller primality test is a probabilistic primality test: an algorithm which determines whether a given number is likely to be prime, similar to the Fermat pri
en.wikipedia.org
주어지는 아파트의 면적을 S라 하면
S = 2xy + x + y
2S = 4xy + 2x + 2y
2S + 1 = 4xy + 2x + 2y + 1
2S + 1 = (2x + 1)(2y + 1)
이다.
따라서 [주어지는 면적] * 2 + 1이 소수라면 두 홀수로 나누어질 수 없기때문에 있을 수 없는 아파트의 면적이 된다.
요약하여, 이 문제는 N * 2 + 1이 소수인지 판별하는 문제이다.
import sys
n = int(input())
answer = 0
# # primelist = [2, 3, 5, 7, 11, 13, 61]
# primelist = [2, 7, 61]
def fastPowMod(a,b,m): # a^b mod m
result = 1
while b > 0:
if b % 2 != 0:
result = (result * a) % m
b //= 2
a = (a * a) % m
return result
def miller_rabin(n, a):
r = 0
d = n-1
while (d % 2 == 0):
r += 1
d = d // 2
x = fastPowMod(a, d, n)
if n == a:
return True
if x == 1 or x == n-1:
return True
for i in range(0,r-1):
x = fastPowMod(x, 2, n)
if x == n-1:
return True
return False
for i in range(n):
S = sys.stdin.readline().rstrip()
S = int(S)
ses = 2 * S + 1
# checklist = [2, 7, 61] # 42억아래 결정적 뭐시기 <- ?
checklist = [2, 3, 5, 7, 11]
flag = True
for i in checklist:
if not miller_rabin(ses, i):
flag = False
break
if flag:
answer += 1
print(answer)
[2, 3, 5, 7, 11]로 밀러-라빈 소수판별법를 진행하였고 이는 (n < 2,152,302,898,747)라면 결과를 보장한다.
'Programming > 알고리즘' 카테고리의 다른 글
| [백준 / Python] 27277번 장기자랑 (1) | 2023.02.05 |
|---|---|
| [백준 / Python] 1925번 삼각형 (2) | 2023.02.01 |
| [백준 / Python] 1780번 종이의 개수 (0) | 2023.01.15 |
| [백준 / Python] 16953번 A → B (3) | 2023.01.11 |
| [알고리즘] 알파벳 피라미드 만들기 (c언어 / 예제) (0) | 2022.02.19 |




댓글